Inclined plane - rolling ball¶
The equation for the acceleration of the center of mass of a rolling sphere on an inclined plane [1] is:
where \(a_{\mathrm{cm}}\) is the acceleration of the center of mass, \(g\) is the acceleration due to gravity, \(\theta\) is the angle of incline, \(I\) is the moment of inertia, \(M\) is the mass and \(R\) is the radius.
The moment of inertia, \(I\) for a hollow sphere [2] is given by
Using this we can simplify the equation for the center mass as follows
Solving for \(\theta\) gives
1) Setting up the photogates¶
Place the two photogates on separate stands [3] on an inclined surface. in this case there were on a smooth glass table top set at a 2.5 degree slope.

2) Software¶
Set-up the software as described in the previous section Using the photogate software.
3) Sample data¶
In the example shown below, we used a ping-pong ball (width = 0.040m) passing through the two photogates on a table with a slope of 2.5 degree. Place the ball on the table above photogate 1 and release so it rolls down the inclined table between the two photogates. Save data for analysis.
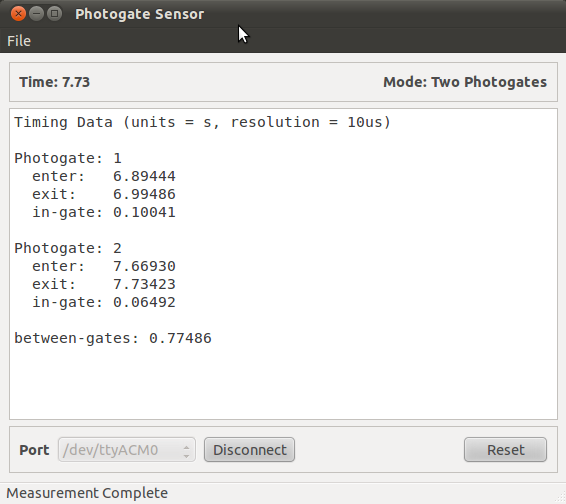
4) Data analysis¶
As in the previous experiment, use data from both photogates to calculate the acceleration, \(a_\mathrm{cm}\) of the ball:
- Velocity in Gate 1 = 0.398 \(\mathrm{m}/\mathrm{s}\)
- Velocity in Gate 2 = 0.616 \(\mathrm{m}/\mathrm{s}\)
- \(a_\mathrm{cm}\) = 0.281 \(\mathrm{m}/\mathrm{s}^2\)
From equation, angle, \(\theta\), is given by
Footnotes
| [1] | http://iweb.tntech.edu/murdock/books/v2chap2.pdf. Example 5 on page 42. |
| [2] | http://en.wikipedia.org/wiki/List_of_moments_of_inertia |
| [3] | Additional equipment from Carolina Biologicals. Support Stand $15.50, Part # 707146 and Clamp Holder, $9.90, Part # 707310 |
